透彻科技
图片来源：infzm.com
据新华社报道，9 月 24 日，在德国海德堡举行的第 6 届海德堡国际数学与计算机科学获奖者论坛上，现年 89 岁的英国著名数学家、阿贝尔奖和菲尔兹奖得主迈克尔·阿提亚，提出了证明黎曼猜想的“简单思路”，并称沿着该思路可以证明黎曼猜想。
阿提亚提出的这个新思路，是基于对物理学中一个重要的无量纲数——精细结构常数的推演，推演过程结合了冯·诺依曼等科学家的早前理论，还引入了一个新的所谓ＴＯＤＤ函数，该函数被视作证明黎曼猜想的核心。不过，阿提亚的证明思路仍有待同行评议。
对于黎曼猜想与区块链的关系，此前有媒体称，“黎曼猜想被证明，基于 RSA 的区块链项目都将湮灭！” 那么，黎曼猜想与区块链究竟有什么关系？若黎曼猜想被证明，对现实世界有什么影响？对区块链有什么影响？
黎曼猜想
首先，我们来看下黎曼猜想是什么。
黎曼猜想是世界七大数学难题之一，由德国数学家伯恩哈德·黎曼于１８５９年提出。黎曼猜想（RH）是关于黎曼ζ函数 ζ(s)的零点分布的猜想。
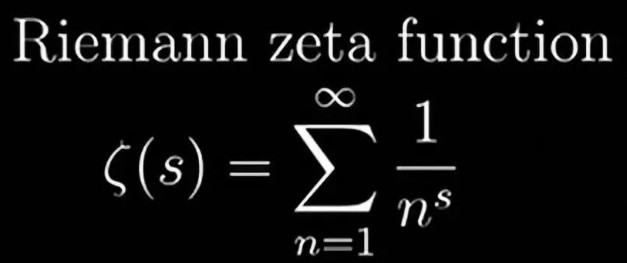
更通俗的数学表达式如下：
ζ（s）= 1 1 / 2^s 1 / 3^s 1 / 4^s ……=0 的所有非平凡解都在直线 x=1/2上。
也即这个猜想是：黎曼函数ζ(s)的全部非平凡零点，全部位于实部为 1/2 的一条直线上。
这里的平凡零点是某个三角 sin 函数的周期零点；非平凡零点是 Zeta 函数自身的零点。
那么黎曼猜想和质数（又叫素数）的分布又有什么关系呢？让我们来看它另一个变形公式：
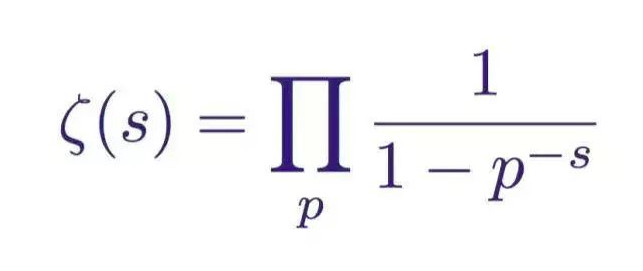公式中的 P 为素数，又称为质数。结合方程与根的关系，这就意味着，这个公式蕴涵着有关素数分布的重要信息。也就是说，该猜想假设了质数分布的规律是“随机而均匀的”，与非平凡零点密切相关。
质数在密码学的应用
那么，为什么要证明质数的分布规律呢？质数如何影响到现实中的应用呢？
质数，在自然数中的分布问题在纯数学和应用数学上都极其重要。
质数指那些只能被 1 和自己整除的整数，而每个整数都能表示成有限个质数的乘积，因此质数可以看做是自然数体系的原子。
在自然数中，越往后，质数的寻找就越难。虽然黎曼猜想假设了质数分布的规律是“随机而均匀的”，但到目前为止也未有人将这一猜想证明。 目前，关于证明这一猜想的最新成果，是一法国团队用计算机，将黎曼猜想推导到 Zeta 函数前十万亿个非平凡零点，均符合了黎曼猜想，无一反例。
于是，数学家将质数的这一特点应用在密码学上。因为人们还没发现质数的规律，以它作密钥进行加密的话，破解者必须要进行大量运算，即使用最快的电子计算机，也会因求素数的过程时间太长而失去了破解的意义。
现在普遍使用于各大银行的是 RSA 公钥加密算法，基于一个十分简单的素数事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。
黎曼猜想若被证明，对现实世界的影响？
虽然这次黎曼猜想并未被完全证明，阿提亚只是提供了一个证明的思路，但若之后被证明，对现实世界会有影响吗？
中国科学技术大学数学系教授欧阳表示，
除非阿提亚证明黎曼猜想不成立，或者提出质数的新规律，否则不会对现实应用产生太大的冲击。
数学是在理论上追求完美，但在现实应用中，很多理论极限上的情况并不会发生。
数论在密码上的应用，包括信息安全和网络空间安全，乃至量子计算，出现的情况都是有限情形（目前使用的质数不超过 150 位数）。黎曼猜想可能的反例出现的范围已经远远超出实际应用中数的范围。
黎曼猜想与区块链之间有什么关系？
密码学的难题有哪些？基于公钥密码体制的经典研究难题，主要有三类：
（1）大整数的质数分解问题（RSA 加密算法属于这个领域）；
（2）椭圆曲线上的离散对数问题(ECDLP)等（椭圆曲线加密算法属于这个领域）；
（3）有限域上的离散对数问题(DLP)；
而区块链项目的加密算法，几乎都是椭圆曲线加密算法，而并未使用 RSA 加密算法。
北京欧链科技有限公司 CTO 宋承根表示，
黎曼猜想是否被证明，都与区块链无关。在区块链中，使用最多的是基于椭圆曲线的相关算法，并不直接与质数相关。椭圆曲线与黎曼猜想或者证明黎曼猜想的工具之间有什么联系，还需拭目以待。